Compartir presentaciones de Keynote en Internet
He estado probando la posibilidad de compartir una presentación hecha con Keynote en Internet y la experiencia es lamentable. Algo que es sencillísimo, rápido y está bien resuelto desde hace años es poco menos que una tortura en el Mac. En esta ocasión Apple tiene que hacer los deberes si de verdad quiere un servicio usable.
El primer problema es que el proceso de creación es eterno. Vale, reconozco que he elegido una presentación larga (94 transparencias), pero ha estado más de media hora para generarla y subirla. Además, en mi caso el archivo a crecido de forma descomunal: de las 140Mb que ocupa el original ha pasado a ¡250 Mb! Excesivo, sobre todo si tenemos en cuenta que la versión en PDF ocupa 38Mb.
Para publicar una presentación desde Keynote, basta con ir al menú «Compartir» y seleccionar la opción «Compartir mediante iWork.com»
Aquí os dejo el resultado.
Mi experiencia: aunque el aspecto final de la presentación es bueno, me parece una herramienta pésima. No creo que la use muchas veces. Servicios como Slideshare le dan mil vueltas.
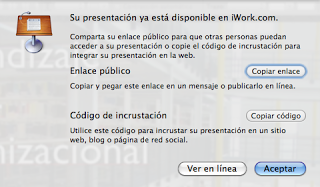
Sólo una cosa más: viendo el código que genera iWork y el enlace público que facilita, parece que a partir del enlace de un recurso, que tiene esta pinta: http://public.iwork.com/document/es/?d=Uso_educativo_de_las_redes_sociales.key&a=p195755206, basta con cambiar «document» por «embed» y sustituir la URL en el código siguiente:
<iframe frameborder=»0″ src=»http://public.iwork.com/embed/?d=Uso_educativo_de_las_redes_sociales.key&a=p195755206&h=768&w=1024&sw=398″ style=»height: 335px; width: 400px;»></iframe>
Hardware basics
Just the slides of these units related with hardware. They’re divided into two parts: the first one related with the processor and the main memory and the second one focused on the input/output devices
Noticias relacionadas