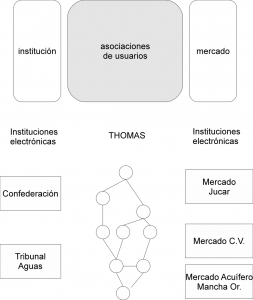
Detrás de este título tan atractivo y motivador se enconde un post… acorde con el título :-) Básicamente la idea es tener algo que nos sirva como ejemplo para empezar a estudiar los espacios de acuerdos y su dinamica en un problema más «Consolider». Y el ejemplo elegido es el modelado de una red fluvial. El propósito es poder usar los modelos de redes de consenso para tratar de modelar las interacciones en un sistema multiagente (SMA) para alcanzar un acuerdo. A través de los espacios de acuerdo puede llegarse a un conjunto de restricciones unidas a las leyes que regulan la propia dinámica del río. Y con algoritmos bien conocidos para resolver problemas de consenso en redes, a partir de su matriz Laplaciana
\(\dot{x} = -Lx \),
donde \(L = [l_{ij}] \) mantiene el grado de los nodos de la red y se define como
\(l_{ij} = -1\) si \(i \neq j\) y \(l_{ij} = |N_i|\) si \(i = j\)
Para poder aplicarlo, es necesario disponer de un modelo de una red fluvial sobre el que se pueda aplicar este formalismo. El modelo de Scheidegger (1967) define la red como un grafo dirigido aleatorio sobre un retículo triangular. En cada intersección, se escoge al azar entre las dos posibles ramificaciones (izquierda o derecha). De esta manera, cada rama del rio es capaz de drenar una superficie de \(\alpha^2\), donde \(\alpha\) es la distancia entre dos vecinos (es decir, que las distancias entre cada segmento de río es de \(\alpha\) -por simplicidad se suele escoger la unidad-).

Por otra parte, para determinar la relación entre el área de drenaje de un río y la longitud de su flujo principal se emplea la Ley de Hawk (1957):
\(l \alpha a^h \centerdot \)
donde l es la longitud del flujo principal, a es el área y el exponente de Hack h se calcula empíricamente y se encuentra en el rango 0.5-0.7. Con estos parámetros, es posible generar aleatoriamente redes que modelan un rio de forma realista, con lo que es posible generar distintos casos de prueba y comprobar empíricamente la validez de las propuestas.
Sobre estos modelos de rios, habrá que distribuir una red de agentes que representen las distintas entidades y personas responsables de la gestión y del consumo de los recursos hídricos. Creo que lo más adecuado es modelarlo como una red de tipo small world que simule las relaciones existentes entre los participantes. de esta forma es posible modelar las relaciones cercanas (entre regantes de una misma comarca) pero también la existencia de posibles relaciones lejanas que podrían modelar incluso a regantes de otras cuencas. Pero esta parte de la red social de riego la dejo para otra anotación
Para más información…
Dodds, Peter Sheridan: Geometry of river networks.- Thesis (Ph.D.)–Massachusetts Institute of Technology, Dept. of Mathematics, 1969. (PDF)
Referencias
J. T. Hack. Studies of longitudinal stream profiles in Virginia and Maryland. In U.S.Geol. Surv.Prof. Pap., 294-B:45–97, 1957.
A. E. Scheidegger. A stochastic model for drainage patterns into an intramontane trench. In Bull. Int. Assoc. Sci. Hydrol., 12(1):15–20, 1967.