Cuando alguien mira al infinito mira lo que está lejos. Asociamos este valor a lo inmensamente grande, al universo. Pero hay otro infinito que se oculta en lo más pequeño, en lo infinitesimal, en ese mundo que se esconde en una imagen de microscopio. Como ese Aquiles recortando en cada paso a la mitad la distancia que le separaba de la tortuga, sin alcanzara nunca (Paradoja de Zenon ).
Ese universo de lo infinitamente pequeño esconde maravillas, artefactos de la mente, objetos que solo existen en el mundo de las matemáticas… o quizá no. Siempre me ha fascinado la gente que es capaz de “ver” con los ojos de la imaginación, que es capaz de construir un modelo mental a partir de un puñado de ecuaciones. Y uno de esos objetos imposibles que a duras penas soy capaz de visualizar es el conjunto de Mandelbrot.
Sin duda es el que se ha llevado la fama, pero si echamos la vista atrás, tenemos una construcción anterior: los conjuntos de Julia. Gaston Julia fue un matemático francés al que debemos los fractales. Lástima que su trabajo sobre iteración de funciones y el concepto de fractal apareciera unas décadas antes de los primeros ordenadores, así que su mirada fue limitada, la que le permitió el lápiz y papel.
El conjunto de Julia se define iterando una función que se conoce como mapa cuadrático: \(z_{n+1} = z_n^2 + c\). Por ejemplo, si \(z_0 = 0\) y \(c = 1\),
$$z_1 = z_0^2 + c = 0^2 + 1 = 1$$
$$z_2 = z_1^2 + c = 1^2 + 1 = 2$$
$$z_3 = z_2^2 + c = 2^2 + 1 = 5$$
y así hasta el infinito y más allá. Pero tiene truco: estos números son números complejos ¿Te acuerdas? Lo de \(\sqrt{-1}\), que no existe y no nos deja resolver ecuaciones de segundo grado. Hay que inventarse una forma de representarlosm, porque aunque se llamen complejos (por cierto, qué nombre más mal elegido), son números normales, que existen y se usan más de lo que crees. Así que cuando te he dicho que \(z_0 = 0\) y \(c = 1\), lo que quería decir realmente es que \(z_0 = 0 + 0i\) y \(c = 1 + 0i\).
Pues bien, el trabajo de Julia consistió estudiar qué ocurría con estas series. Había valores de \(z_0\) que hacían que los valores fueran cada vez mayores, mientras que otros se quedaban dentro de unos límites. Por ejemplo , si \(z_0 = 1\) y \(c = -1\),
$$z_1 = z_0^2 + c = 1^2 -1 = 0$$
$$z_2 = z_1^2 + c = 0^2 – 1 = -1$$
$$z_3 = z_2^2 + c = (-1)^2 -1 = 1 – 1 = 0$$
$$z_4 = z_3^2 + c = 0^2 – 1 = -1$$
Como ves, hemos entrado en un bucle y vamos a estar siempre entre 0 y \(-1\). En este caso \(z_0 = 1\) pertenece al conjunto de Julia. Lo interesante de este conjunto es que no tiene unos límites claros, y de ahí vienen los fractales. En la frontera, cambios en decimales muy pequeños pueden hacer que el punto pertenezca o no al conjunto, y no se puede saber a priori sin calcularlo.
¿Qué tiene que ver Mandelbrot con todo esto? Una de sus inquietudes era clasificar todas las formas posibles que tenían los conjuntos de Julia. Una manera de hacerlo es elegir un valor de \(z_0\) fijo, por ejemplo \(z_0 = 0\), y ver qué pasa cuando cambiamos c. En este caso, el valor se queda dentro de un círculo de radio 2 o crece de forma ilimitada. Los matemáticos Robert Brooks y Peter Matelski obtuvieron por primera vez una imagen de ese conjunto usando un ordenador, y lo publicaron en un artículo en 1978.
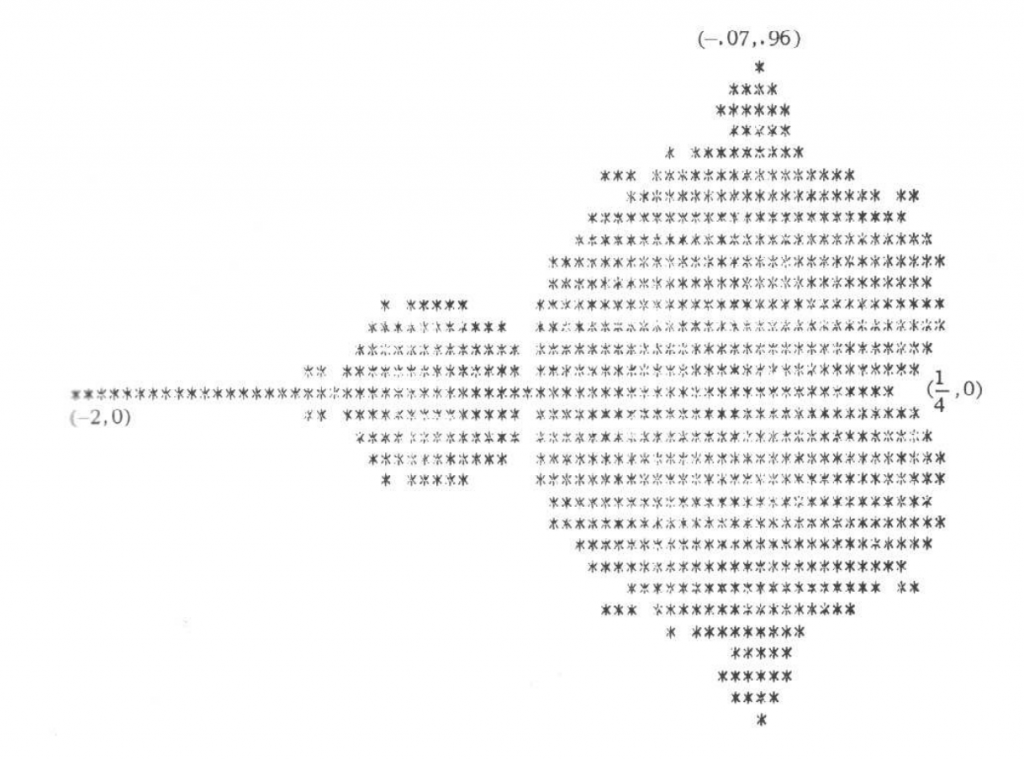
Este trabajo pasó desapercibido hasta que Mandelbrot lo replicó usando un ordenador con capacidades gráficas, surgiendo la figura típica que habrás visto miles de veces. Lo maraviloso de la figura es su gran complejidad, el nivel de detalle al que puedes llegar, su estructura fractal, la autosemejanza que emerge constantemente.
Así qiue me he venido arriba, y para compensar la chapa, te dejo el código para generar el conjunto de Mandebrot.
- el código que genera la imagen del artículo original de Brooks y Matelski.
- el código que genera la versión gráfica con una resolución mayor.
- un código para poder hacer ampliar las zonas que desees para ver los detalles.
Y también te dejo un documental de Arthur C. Clarke sobre este conjunto, en el que aparece el propio Mandelbrot hablando de él.
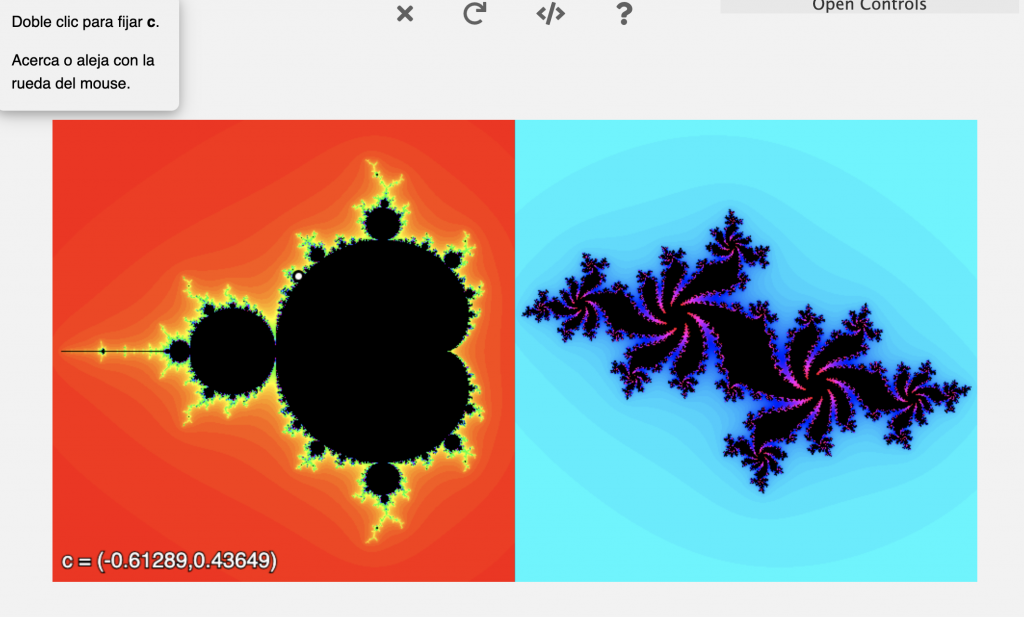
¡Ah! y por si no tienes suficientes miradas, te he hablado de la relación entre el conjunto de Mandelbrot y el de Julia. Se puede considerar que el primero es una especie de índice sobre el tipo de soluciones del segundo, y puedes explorar qué aspecto tiene el conjunto de Julia correspondiente al valor de z situando el ratón en el punto que quieras del conjunto de Mandelbrot. pincha sobre la imagen para acceder a la web.
Esta entrada forma parte de #Polivulgadores de Café Hypatia en su edición de julio de 2023, con el tema «Miradas«.
Para saber más
Robert Brooks y Peter Matelski, The dynamics of 2-generator subgroups of PSL(2,C), in Riemann Surfaces and Related Topics: Proceedings of the 1978 Stony Brook Conference Irwin Kra (ed.).
Benoît Mandelbrot. La GeometrIa fractal de la naturaleza. Tusquets Editores S.A. (2021)
James Gleick. Caos: la creación de una ciencia. Ed. Crítica (2012)
Bartosz Zaczyński. Draw the Mandelbrot Set in Python [en línea] Disponible en https://realpython.com/mandelbrot-set-python/