O al menos sin compartirlos a desconocidos. Los procesos de consenso en redes permiten hacer cálculos de forma descentralizada trabajando con información local (privada) y compartiéndolo solo con los contactos directos.
En estos días se ha hablado mucho del modelo chino y coreano y de cómo estos países han logrado controlar la expación del SARS-CoV-2 (en adelante coronavirus, que ya es casi como de la familia). Una de las medidas estrella ha sido una aplicación móvil que ha usado el gobierno de Corea del Sur para hacer un seguimiento de la infección y controlar a los pacientes. Usando un código de color para identificar el riesgo y con medidas estrictas para las personas infectadas, han conseguido frenar la fase de crecimiento de la enfermedad, y por lo visto mejor que nosotros.
Pero una de las principales críticas es el uso que se haga de esos datos. Esos países tienen fama de usar los datos públicos para controlar a sus habitantes y, en casos como este, de emergencia nacional, la gente suele estar dispuesta a sacrificar sus libertades. Por ejemplo, en una encuesta sobre el uso de datos móviles y de salud que lanzó Victoriano Izquierdo en Twitter, el 75% estaba dispuesto a permitirlo (yo soy del otro 25%)
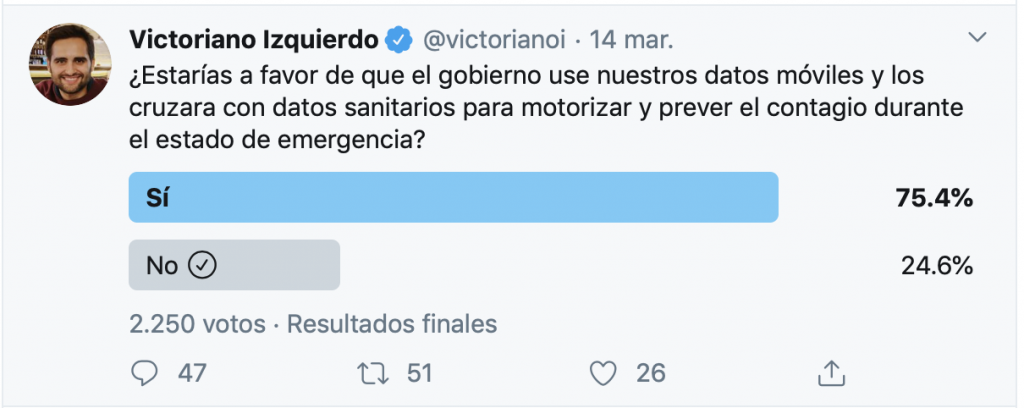
Esto me llevó a pensar ¿es posible conseguir esa misma información sin la necesidad de compartir la información sensible, como son los datos sanitarios? Y entonces es cuando se me encendió la lucecita y caí en que se puede utilizar todo el trabajo de mi tesis, y en concreto, la parte que tiene que ver con votaciones distribuidas, que ya conté por aquí (por cierto, a ver si me pongo, que os había prometido una serie de entradas sobre todo eso).
Procesos de consenso en redes
No voy a contar otra vez con detalle todo el proceso de consenso (si te interesa está en las entradas anteriores), pero lo recordaré para recién llegados. El consenso es una forma de distribuir información en una red que permite hacer cálculos de forma distribuida, utilizando la información propia y la que proviene de los vecinos directos. A partir de un proceso iterativo: calcular-compartir-calcular-compartir… al final se llega a un estado en el que los valores que tiene la red ya no cambian y has completado el cálculo.
Imagínate que quieres saber la edad media de los usuarios de Twitter. Hay dos posibilidades: o lo calcula Twitter (que es la única que tiene todos los datos, como el gobierno de Corea del Sur) o uso esta estrategia de consenso. ¿Qué hay que hacer? Es sencillo
- cada persona pasa su edad a sus contactos (como son sus amistades, en principio no hay problema)
- cada persona, recalcula la edad de la red de la siguiente manera: \(edad(t+1) = edad(t) + \varepsilon \sum edadvecino_j(t) – edad(t)\) que se podría traducir como «mi edad más la suma de las diferencias de mi edad con las de mis contactos»
y todo esto se repite hasta que la edad no cambia. Está demostrado que esto converge (se detiene tras un número suficientemente alto de iteraciones) y que el resultado final es la media de las edades iniciales. Y todo esto sin nadie que controle ni tenga todos los datos. Además, date cuenta de que, excepto en el primer intercambio, en el que le pasas tu edad real a tus contactos, el resto empieza a ser información agregada de la que no se puede asilar los datos de una persona en particular.
¿Cómo se aplica para el caso del coronavirus?
Siguiendo este mismo procedimiento, si en lugar de la edad cada persona intercambia su situación de riesgo, el resultado que obtenemos es el riesgo medio de toda la población. Sin duda es útil, pero eso no da la información de la aplicación coreana sobre el riesgo en una determinada zona. Para eso hace falta poder segregar a las personas por sectores y agrupar los datos de cada uno. Y para ello se puede utilizar la misma estrategia que para las votaciones, con un ligero cambio.
Lo primero, hay que dividir el área que queremos estudiar en una rejilla. No habría problema en usar otros límites, aunque sean irregulares: municipios, barrios, manzanas…
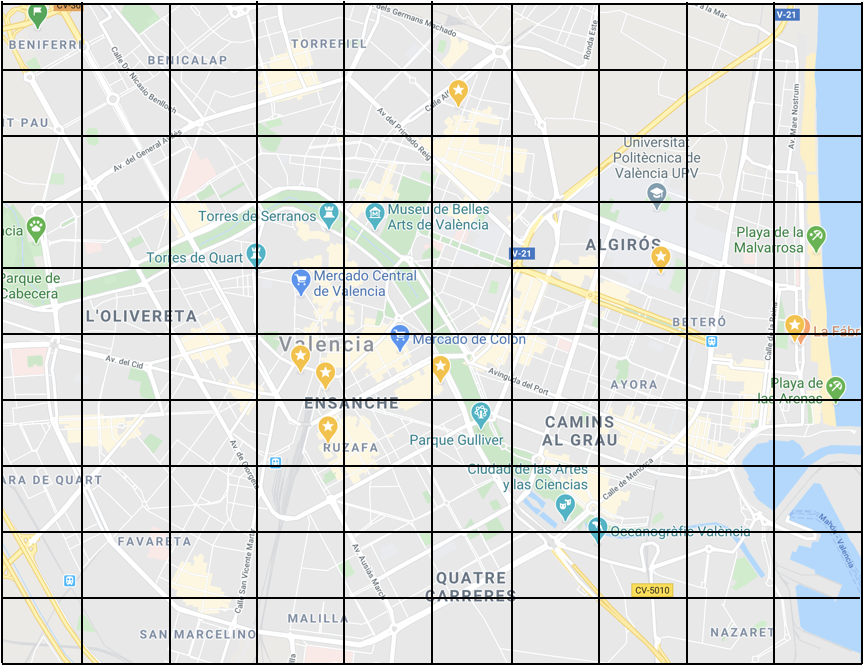
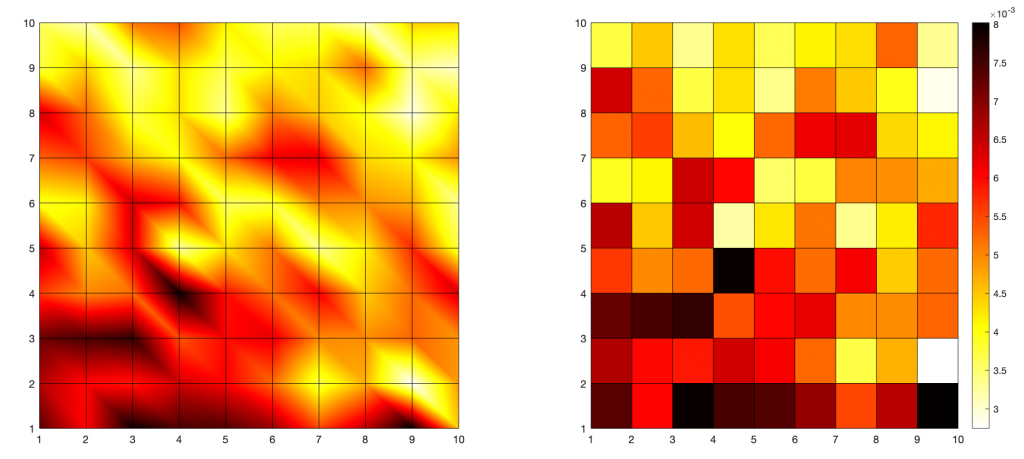
Lo que va a intercambiar cada persona es una lista de valores, tantos como casillas. En este caso, como es de 10×10, tenemos una lista de 100 valores. El primer valor (el equivalente a la edad) es el índice de riesgo que tiene la persona en la casilla que le corresponde a su ubicación, y todo lo demás a cero. Voy a asumir que el valor de riesgo es un número entre 0 (ningún riesgo – blanco) y 1 (riesgo máximo – negro).
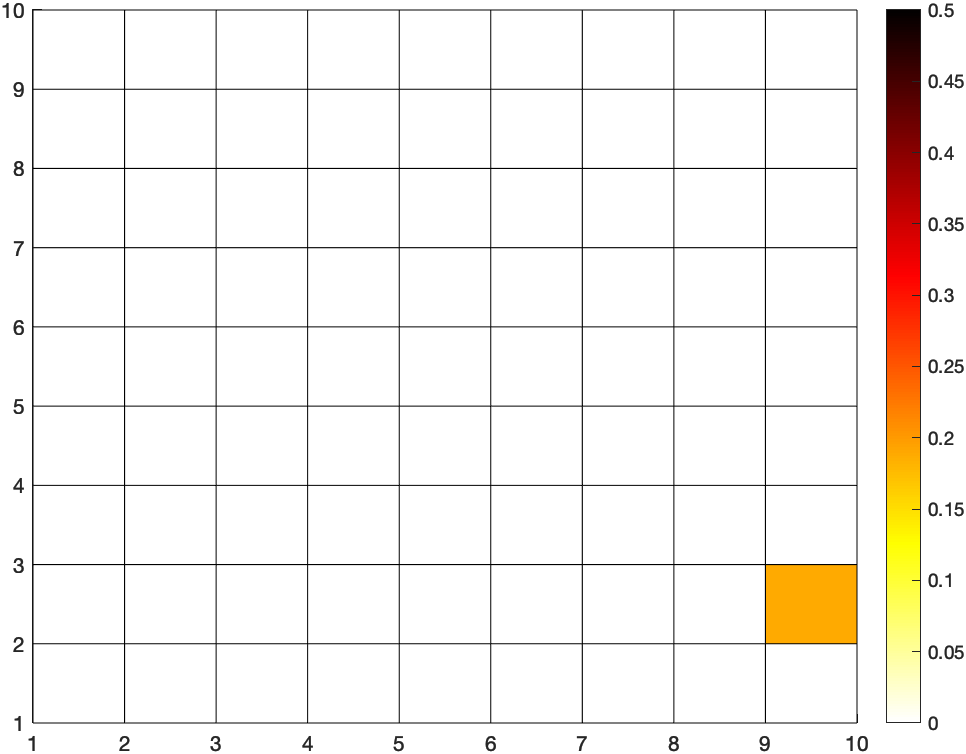
A esa lista le añado un valor más que me va a permitir contar cuántas personas hay en la red. Este valor estará inicializado a 0 en toda la red excepto en un nodo arbitrario. Así, el valor inicial de cada nodo de la red es
\(x_i(0) = \langle r_1, r_2,\ldots, r_{100} | 0 \rangle\)
A partir de aquí, solo hay que aplicar la ecuación del proceso de consenso en cada uno de los nodos de la red una y otra vez hasta que los valores se estabilizan y no cambian, haciendo
\(x_i(t+1) = x_i(t) + \varepsilon \sum_{j \in N_i} x_j(t) – x_(t)\)
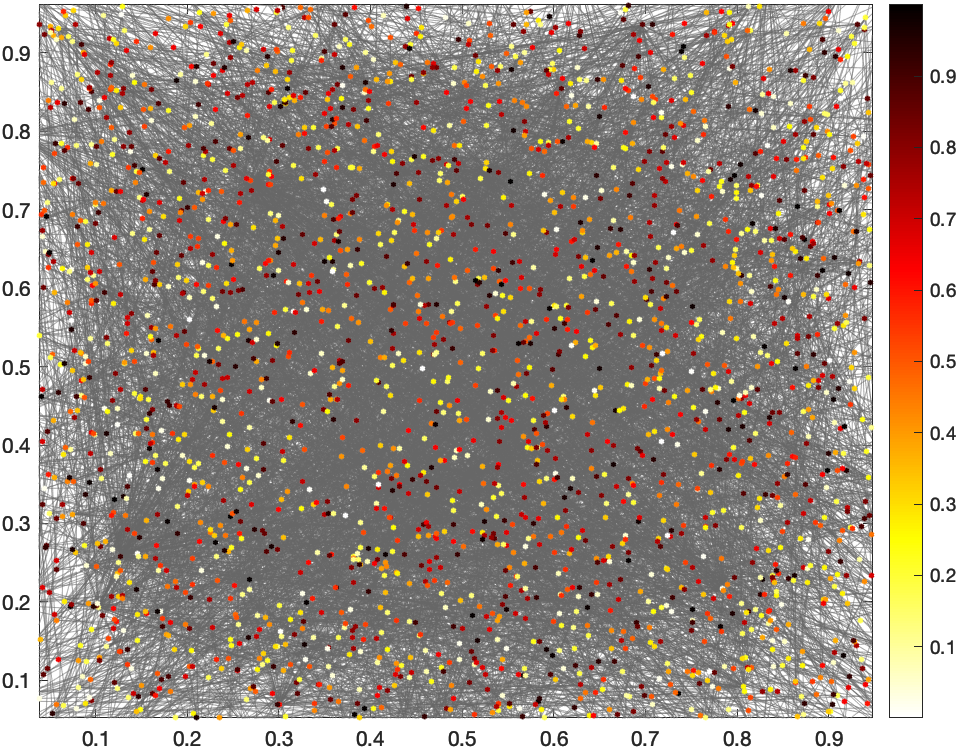
El valor de \(\varepsilon\) es una constante que depende del grado máximo de la red, pero también se puede calcular sobre la marcha, así que no hay problema. El resultado es un mapa como el siguiente, en el que están acumulados los índices de riesgo en cada celda
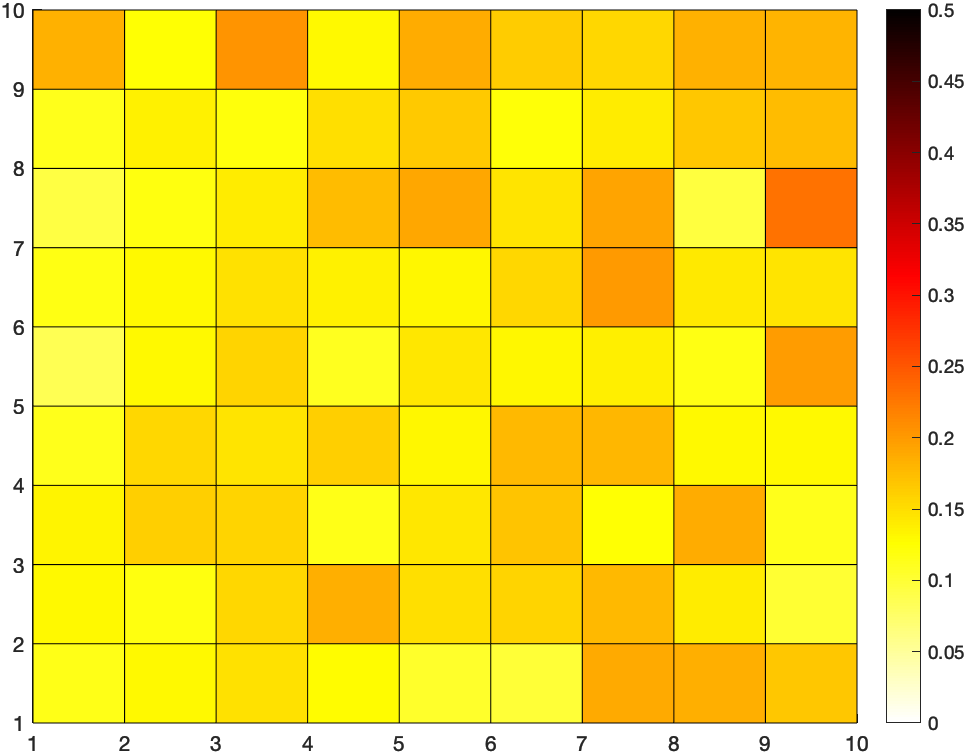
Lo importante de todo esto es que solo has intercambiado tu índice de riesgo con tus contactos directos, que normalmente son tu familia, amigos y compañeros de trabajo. Si te hubieras contagiado, son las personas a quien se lo comunicarías de todas formas. Y esta información solo está disponible en el primer intercambio. A partir de ahí, empiezan a ser valores agregados y no es posible (sin apoyo de otra información) identificar la información privada de una persona en particular.
¿Cómo puede la administración conseguir estos datos? Basta con unirse a la red y al final obtendrá el mismo mapa que el resto de usuarios.
¿Cómo funciona?
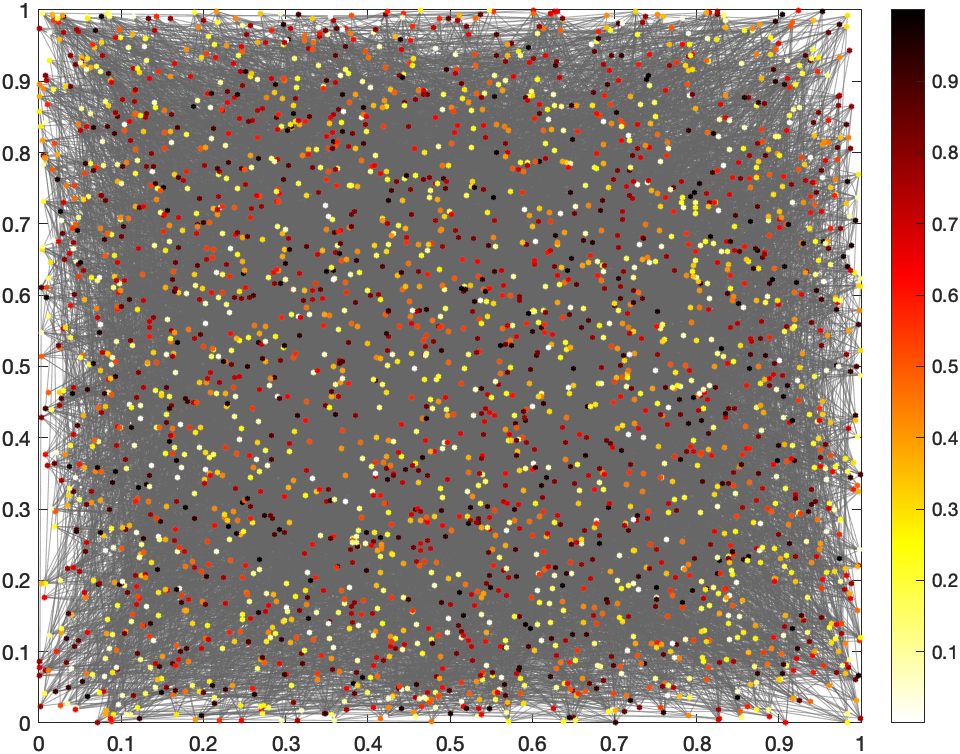
He hecho algunas pruebas para que veas como funciona esto, porque la teoría es muy sufrida y lo aguanta todo. Para simularlo, he buscado la densidad de población del área metropolitana de Valencia, que son unos 3.200 hab/km2, así que he creado una red de 3000 nodos. A la hora de conectarlos, he hecho pruebas con 4 tipos de redes
- una red aleatoria: los nodos se conectan al azar con cualquier nodo de la red con la misma probabilidad. La densidad de enlaces es la suficiente para que se forme la componente gigante (log(n)/n)
- una random geometric network (RGG): es una red donde los nodos se distribuyen de forma aleatoria en un cuadrado de lado 1. Luego se conectan a los nodos que estén dentro de un radio determinado. En mi caso, para mi el área es de 1 km2 y el radio para enlazar dos nodos es de 50 m (0,05)
- una variante de la RGG añadiendo un enlace de larga distancia con una probabilidad inversa a la distancia que los separa (más improbable cuanto más lejos estén), parecido a lo que hace el modelo de Kleinberg
- una red con preferential attachment (Barabási-Albert), para modelar mejor las relaciones entre las personas, donde aparece el efecto de small world y la distribución del grado de la red sigue una ley de potencias.
Una nota importante: la topología de la red no afecta al resultado. Uses la red que uses, converge al mismo valor. En este caso, al mapa que aparece arriba. La única diferencia, como verás a continuación, es en la velocidad de convergencia.
Red aleatoria
La red aleatoria la he usado sobre todo para tener una referencia sobre la que comparar las demás. No tiene más interés, ya que las redes de interacción entre las personas no son aleatorias. Pero sirve para hacer ejemplos sencilos y comprobar que las cosas funcionan
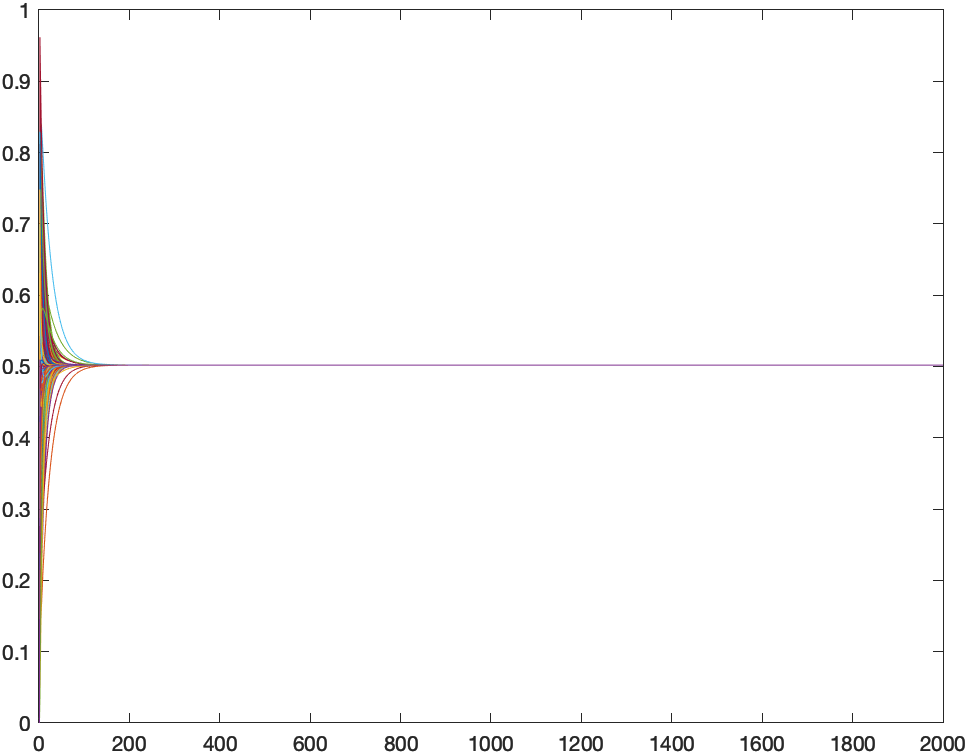
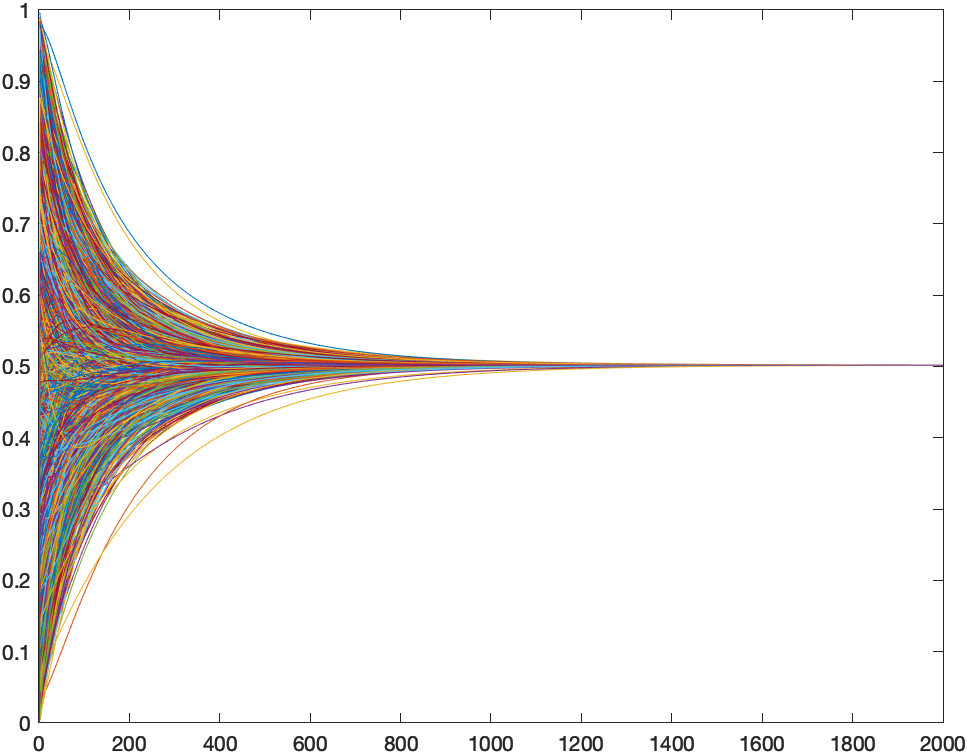
A la izquierda está la red aleatoria y a la derecha el proceso de consenso. He utilizado 2000 iteraciones para que todos estén en la misma escala, pero se puede ver cómo en apenas 200 esta red ya tiene el valor final. Es decir, con 200 intercambios de datos ya se puede obtener el mapa completo.
Random geometric graph (RGG)
El interés de esta red es probar qué pasa si me uno a las personas que están a mi alrededor. Normalmente van a ser personas que conozco (a no ser que esté conectado mientras me muevo por la calle… bueno, cuando se podía ;-) La limitación es que de vez en cuando entro en contacto con alguien lejano.
Para solucionarlo, una pequeña variante consiste en añadir un enlace con un nodo lejano al azar. La probabilidad de unirme a ese nodo es inversamente proporcional a la distancia entre los dos. El efecto es que suele tener en la red es el de acortar mucho la longitud de los caminos y el diámetro de la red. Aunque no sea lo más ortodoxo (hay artículos en los que oirás hablar de los vuelos de Levy y de patrones de movilidad recurrentes) me vale para esta prueba.
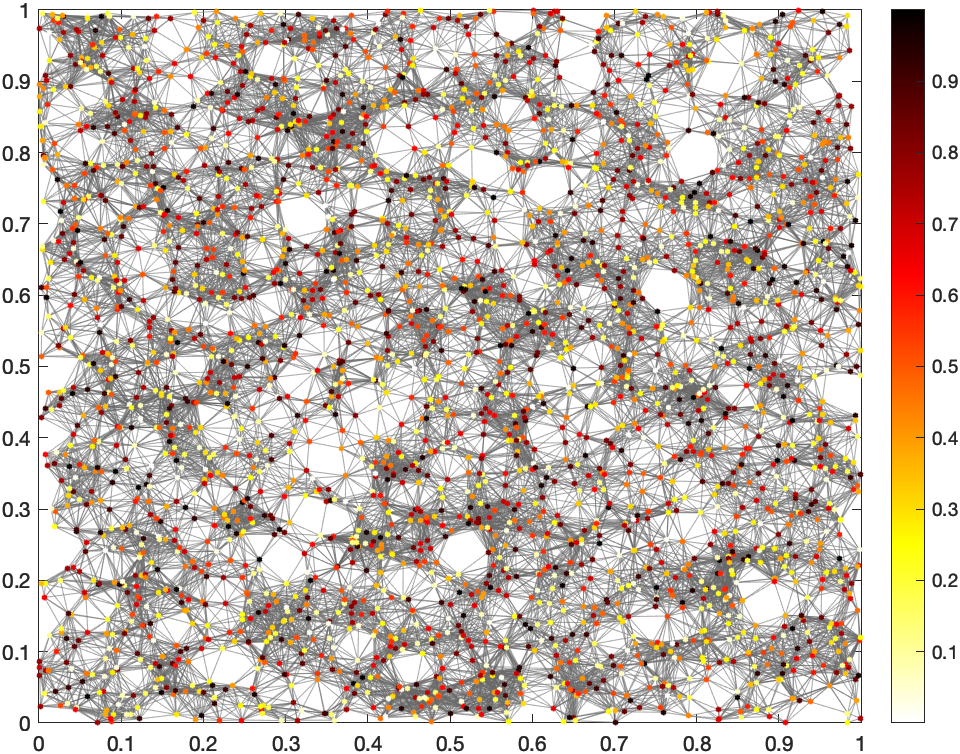
RGG 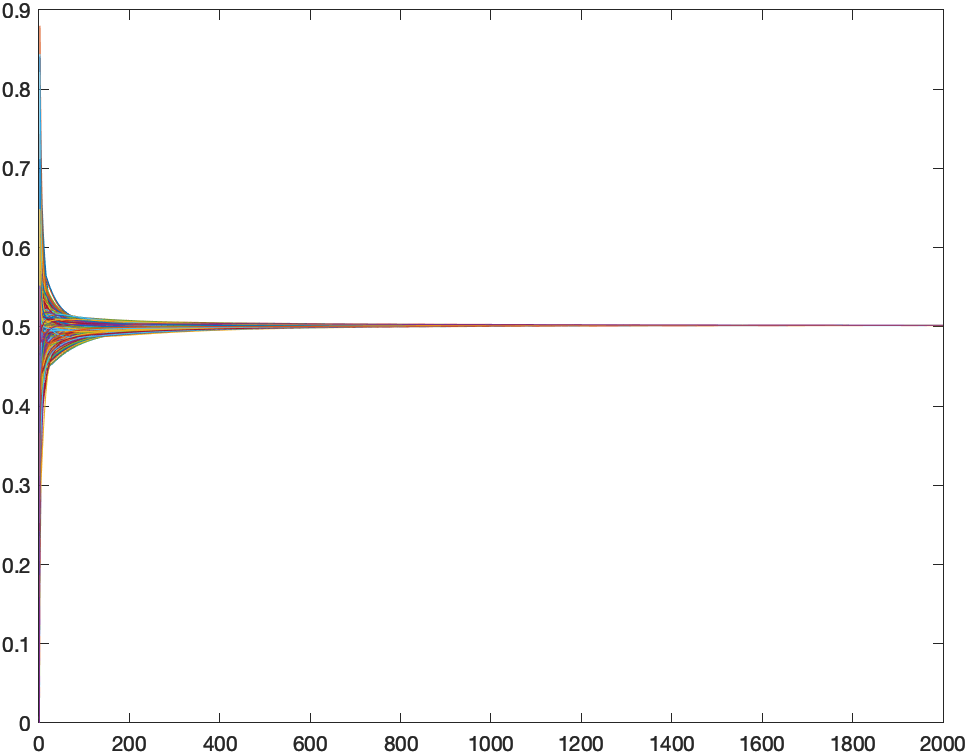
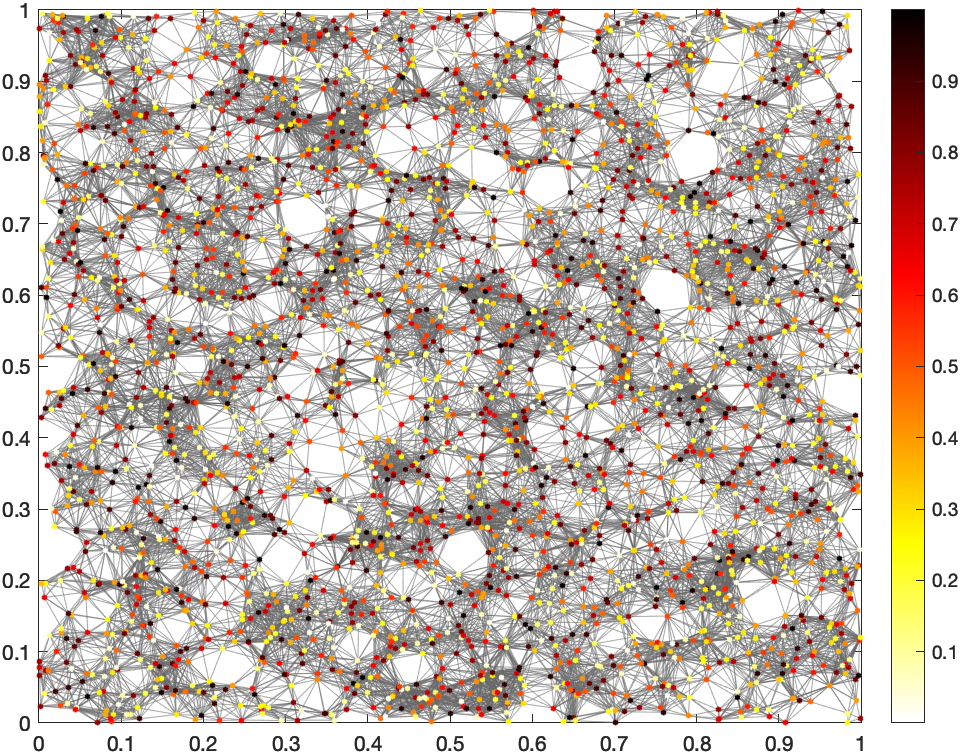
RGG ampliada con enlaces largos 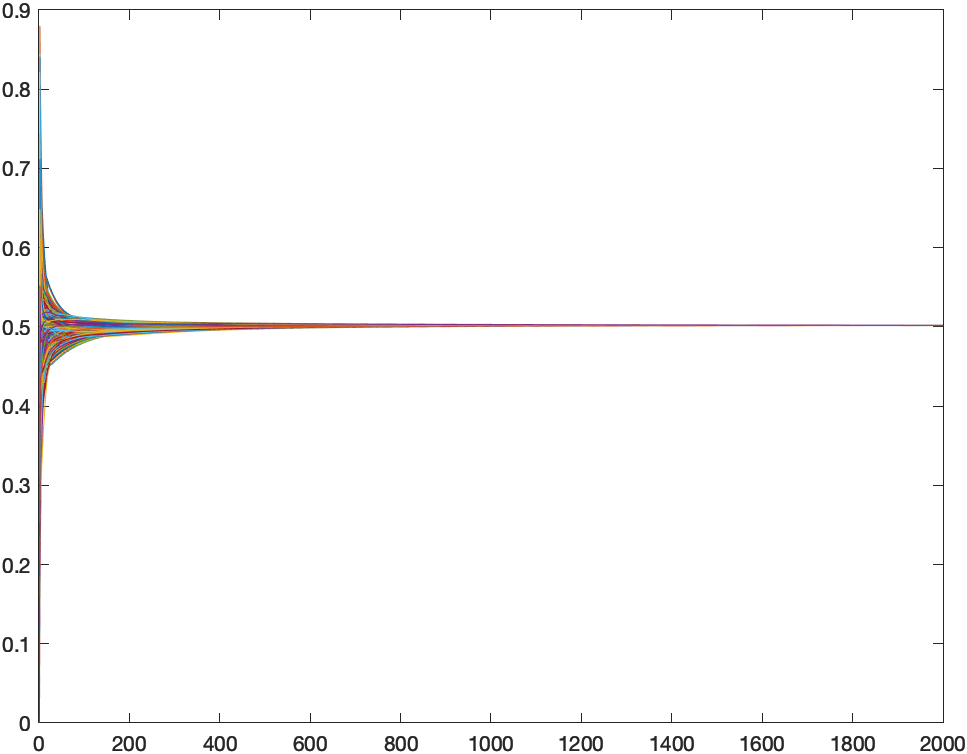
Aquí se puede ver cómo apenas hay diferencia entre los dos casos. La velocidad de convergencia es menor que en una red aleatoria. Con 500 iteraciones todos los nodos de la red están ya bastante cerca de tener el mapa definitivo, pero hacen falta unas 1000 para que se haya propagado por toda la red con una buena precisión
Red con preferential attachment
Es la red típica cuando se analizan redes complejas. Las propiedades de la distribución de grado como una ley de potencias y el efecto de small world son característicos de muchas redes naturales y artificiales, y también de las relaciones en redes sociales. Es uno de los modelos más realistas que podemos construir ¿Qué efecto tiene en el consenso? Pues que el proceso converge más despacio.
Se ve claramente cómo a los nodos les cuesta llegar a ese valor de consenso y necesitan casi 1500 iteraciones para llegar a unos valores cercanos al mapa final definitivo. Una forma rápida de acelerar el consenso en esta red es aumentar el número de conexiones. En este ejemplo cada nodo se conecta a otros dos. Si lo aumentas, por ejemplo a diez conexiones (eso equivaldría a relacionarse con 3.000 personas en una ciudad de 1.000.000 de habitantes) la red converge en 600 pasos. De todas formas, en un ordenador estamos hablando de segundos (pocos).
Así que, para hacer una aplicación real, habría que decidir qué modelo de red interesa más: si uno que emplea la información de los vecinos cercanos dentro de un radio determinado o la red de contactos real.
¿Cómo se construye este modelo?
Puedes programarlo de muchas maneras. Yo lo he hecho con Matlab y en lugar de implementar los nodos de forma independiente he empleado una notación matricial que hace el código más conpacto y eficiente. Eso no impide una implementación completamente distribuida y se puede programar sin problema las fórmulas de arriba para Android o iOS.
En primer lugar, indicamos el tamaño de la red (n), el valor de riesgo de cada nodo, que lo genero al azar entre 0 y 1, y las coordenadas de cada nodo, que también es un par entre 0 y 1. Así todos los nodos se encuentran en el área de un cuadrado de lado 1, que podemos reescalar sin problema para adaptarlo a cualquier área.
clear; n = 3000; % population x0 = rand(n,1); % initial risk contagion values coor = rand(n,2); % coordinates of each node
Generar una red aleatoria es sencillo: solo hay que proporcionar la densidad de enlaces (p) y con eso Matlab ya tiene una función que nos genera una matriz dispersa (para que ocupe menos) aleatoria y simétrica (red no dirigida) con esa densidad. Luego solo habría que asegurarse que la diagonal no tiene ceros, para evitar arcos sobre el propio nodo.
p = log(n) / n; % network density A = spones(sprandsym(n,p)); A(1:1+n:n*n) = 0;
Si lo que quieres generar es una RGG, Matlab también te lo da casi hecho. La función pdist() te devuelve una matriz las distancias entre todos los pares de valores (en mi caso, las coordenadas). Con find() me quedo con los nodos que están a menos de una distancia dada (0.05, que equivalndría a 50 m) y por último construyo una matriz dispersa que conecte los nodos seleccionados. Como en el caso anterior, elimino los elementos de la diagonal para evitar bucles.
max_distance = 0.05; distances = squareform(pdist(coor)); [row,col] = find( distances < max_distance ); A = spones(sparse([row;col],[col;row],1,n,n)); A(1:n+1:n*n) = 0;
La red de preferential attachment es un poco más largo, pero la dejaré también disponible. Si quieres ver cómo es la red que has generado, se puede mostrar de la siguiente forma.
p = plot(graph(A),'XData',coor(:,1),'YData',coor(:,2),
'NodeCData',x0,'EdgeColor','#cccccc');
colormap(flipud(hot)); % change de colors of the plot
colorbar; % shows the color bar
axis([0 1 0 1]); % adjust the axis to an 1x1 square
[r,c] = find(A); % just to export the graph to csv
csvwrite("covid.csv",[r c]);
Eso genera las redes que has visto arriba. El siguiente paso es crear la rejilla sobre el mapa. Creo tantas como nodos (realmente es una matriz tridimensional) y cada uno añade su valor de riesgo en las celda de la rejilla según las coordenadas en las que se encuentra.
grid_size = 10;
loc = ceil(coor * grid_size);
status = zeros(n,grid_size,grid_size);
for i = 1:n
status(i,loc(i,1), loc(i,2)) = x0(i);
end
Ahora está todo listo para hacer el consenso. Como he comentado, empleo la forma matricial porque es más eficiente en Matlab, pero es exactamente igual que la distribuida. La dinámica del consenso se rige por la laplaciana (L) de la matriz de adyacencia del grafo. Si fuera un modelo continuo y lo resolviéramos con ecuaciones diferenciales no había que hacer nada más. Pero como se trata de un proceso iterativo discreto, donde se va recalculando la solución iteración a iteración hasta que converge, la matriz que se emplea es la de Perron-Frobënius (P). Convierto las rejillas en vectores para que se pueda hacer el consenso en un solo paso con reshape() (me quedan n vectores de 100 elementos) y ejecuto las iteraciones del proceso de consenso ue marca iter. La expresión matricial \(x(t+1) = P x(t)\) es equivalente a ejecutar el consenso individual en cada nodo con la fórmula de arriba.
L = diag(sum(A)) - A; % Laplacian of A
eps = 1 / max(diag(L)) * 0.99; % eps < 1 / max(degdree)
P = eye(n) - eps * L; % Perron matrix P = I - e*L
iter = 2000; % number of iterations
x = reshape(status,[n,grid_size*grid_size]); % initial risk
for i = 2:iter
x = P * x;
end
x = x * n;
Cuando el proceso acaba, todas las filas de x son iguales, lo que quiere decir que cada nodo conoce la solución final. Repito que esto es un modelo centralizado de lo que habría ocurrido en distribuido para simularlo de forma eficiente. Para ver el resultado, tomamos cualquier vector (yo cojo el primero), volvemos a recuperar la forma original con otro reshape() y lo mostramos en un mapa de superficie. Ten en cuenta que en el gráfico los valores están en los vértices de la rejilla, así que para verlo mejor puedes interpolarlo.
map = reshape(x(1,:,:),[grid_size,grid_size]); [gx,gy] = meshgrid(1:grid_size); surface(gx,gy,map,'FaceColor','interp'); colormap(flipud(hot)); colorbar;
Si quieres obtener el código, lo he dejado disponible en el repositorio de mi grupo de investigación. Puedes acceder en este enlace: http://gitlab.gti-ia.dsic.upv.es/mrebollo/covidcons
Resumiendo
La información de salud es una información sensible que no todos los usuarios desean compartir. Sin embargo, hay ocasiones, como la epidemia actual CoVid-19 en la disponer de esos datos puede ser vital a la hora de controlar la enfermedad. Se entiende perfectamente la preocupación de los usuarios por el tratamiento de sus datos personales y el uso futuro que se pueda hacer de ellos por parte de los gobiernos, de la empresa responsable de la aplicación o por el posible robo de datos.
Por todo ello, es deseable una solución que minimice los datos que se hacen públicos. Los procesos de consenso en redes permiten obtener información útil para la adminnistración en el caso de la epidemia, sin sacrificar la privacidad de la ciudadanía.
Cada persona puede calcular su estado de salud y determinar un valor de riesgo que puede compartir con sus contactos más directos: familia, amigos y compañeros de trabajo principalmente, que sos personas a las que de todas formas comunicaríamos un contagio. Luego, el proceso de consenso agrega esos datos y permite construir un mpa de riesgo a partir de la información proporcionada. Ese mapa se construye de forma iterativa mientras se propaga por toda la red y cuandose completa todas las personas disponen del mapa. No es necesaria ninguna base de datos centralizada ni ninguna entidad que controle el proceso.



¿Cómo puedes modelar el efecto del distanciamiento social? Este conlleva una reducción drástica de los contactos con terceros.pero losincrementa dentrobde los grupos familiares.(confinados) y conocer el balance entre estos dos efectos es esencial para predecir su efectividad.